Множество элементов называется линейным (векторным) пространством, если на этом множестве выполнено 3 условия:

• Введена операция суммы
  $\forall x, y, \in L \quad Z = x + y, z \in L$
• Операция умножения элеменента на число
  $\forall x \in L, \forall \lambda \in R \quad y = \lambda x, y \in L$
• Выполнено 8 аксиом
  1. $x + y = y + x \quad \forall x,y \in L$
  2. $x+(y+z)=(x+y)+2 \quad \forall x,y,z \in L$
  3. $\exists \theta \in L: \forall x \in L \quad x+\theta=x$
  4. $\forall x \in L \exists (-x) \in L:x+(-x)=\theta$
  5. $\lambda (x+y) = \lambda x + \mu x \quad \forall x \in L \quad \forall \lambda,\mu \in R$
  6. $\lambda (\mu x) = (\lambda \mu)x \quad \forall x \in L \quad \forall \lambda,\mu \in R$
  7. $\lambda (\mu x) = (\lambda \mu) x \quad \forall x \in L \quad \forall \lambda,\mu \in R$
  8. $1*x=x\quad \forall x\in L$

$x - y = x + (-y)$ - определение разницы
Нормированное линейное пространство - линейное пространство L, в котором каждому элементу $x$ из $L$ поставлено в соответствие действительное число, называемое нормой $||x||$ , причём выполняется 3 условия (аксиомы нормы):

1. $\forall x \quad ||x|| \ge 0, ||x||=0 \rightarrow x = \theta$
2. $||\lambda x|| = |\lambda| * ||x|| \quad \forall \lambda \in R, \forall x \in L$
3. $||x+y|| \le ||x||+||y||$
   Расстояние между элементами x и y линейного нормированного пространства - норма разности этих элементов
   $\rho (x,y) = ||x-y||$

Нормированное пространство n-мерных векторов

• Кубическая норма
  $||\overline{x}||_\infty = max\{|\overline{x_n}|\} = max\{|x_1|,|x_2|,...|x_n|\}$
• Октаэдрическая норма
  $\displaystyle||\overline{x}||_1 = \sum_{1}^{i}|x_i| = |x_1|+|x_2|+...+|x_n|$
• Сферическая (Евклидова) норма
  $\displaystyle||\overline{x}||_2 = \sqrt{\sum_{i}|x_i|^2} = \sqrt{|x_1|^2+|x_2|^2+...+|x_n|^2}$
  $\overline{X}=\begin{pmatrix}1\\2\\-3\end{pmatrix}$ $\overline{Y}=\begin{pmatrix}1\\-1\\1\end{pmatrix}$ $\overline{X}-\overline{Y}=\begin{pmatrix}0\\3\\-4\end{pmatrix}$
  $\rho(\overline{x},\overline{y})=||x-y||=\begin{cases}||x-y||_\infty=4\\||x-y||_1=7\\||x-y||_2=\sqrt{9+16}=5\end{cases}$

Нормы для векторов + нормы для матриц

$\overline{X}=\begin{pmatrix}x_1\\\vdots\\x_i\end{pmatrix}\quad||\overline{x}||=1$

1. $||\overline{x}||_\infty=1$:
   $|x_1|=1\to|x_2|\leqslant1$
   $|x_2|=1\to|x_1|\leqslant1$

   

2. $||\overline{x}||_1=|x_1|+|x_2|=1$
   $\ \ \ x_1+x_2=1\to\quad x_1\geqslant0,\quad x_2\geqslant0$
   $\ \ \ x_1-x_2=1\to\quad x_1\geqslant0,\quad x_2<0$
   $-x_1+x_2=1\to\quad x_1<0,\quad x_2\geqslant0$
   $-x_1-x_2=1\to\quad x_1<0,\quad x_2<0$

   

3. $||\overline{x}||_2=\sqrt{|x_1|^2+|x_2|^2}=1$
   $x_1^2+x_2^2=1$

   

$||\overline{x}||_\infty\leqslant||\overline{x}||_2\leqslant||\overline{x}||_1\leqslant n*||\overline{x}||_\infty$
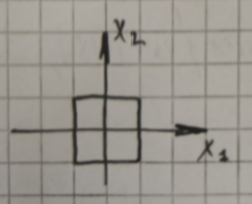
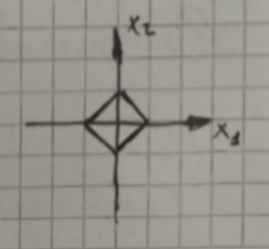
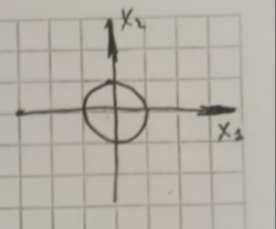
$\overline{X}$ - точное значение вектора
$\overline{x^*}$ - приближённое значение вектора
$\overline{\Delta x^*}=||\overline{X}-\overline{x^*}||$
$\delta x=\dfrac{\Delta x}{||\overline{X}||}\quad\delta x^*=\dfrac{\Delta x^*}{||x^*||}$

$A_{m*n}=\begin{pmatrix}a_{11}& a_{12}& \dots & a_{1n} \\ a_{21}& a_{22}& \dots & a_{2n} \\ \dots&\dots&\dots&\dots \\ a_{m1}& a_{m2}& \dots & a_{mn} \end{pmatrix}$

$||A||=sup\dfrac{||A*\overline{x}||}{||\overline{x}||},\quad\overline{x}\ne\theta$

1. $||A||_\infty=\underset{i}{\max}\underset{j}{\sum}|a_{ij}|$ (Сумма по строкам)
2. $||A||_1=\underset{j}{\max}\underset{i}{\sum}|a_{ij}|$ (Сумма по столбцам)
3. $||A||_2=\sqrt{\underset{i}{\sum}\underset{j}{\sum}|a_{ij}^2|}$

Доказательство бесконечной нормы для матриц + определение погрешностей для матриц

Число обусловленности матрицы А - количественная оценка согласованности матрицы¹

$A_{m*n}*\overline{X}=\begin{pmatrix}a_{11}& a_{12}& \dots & a_{1n} \\ a_{21}& a_{22}& \dots & a_{2n} \\ \dots&\dots&\dots&\dots \\ a_{m1}& a_{m2}& \dots & a_{mn} \end{pmatrix} * \begin{pmatrix}x_1\\x_2\\\vdots\\x_n\end{pmatrix}\quad\begin{pmatrix}i=1\dots m\\j=1\dots n\end{pmatrix}$
$||A\overline{X}||_\infty=\underset{i}{\max}|\underset{j}{\sum}a_{ij}x_j|\leqslant\underset{i}{\max}\underset{j}{\sum}|a_{ij}|*|x_j|\leqslant\underset{i}{\max}\underset{j}{\sum}|a_{ij}|\underset{j}{\max}|x_j|=\underset{j}{\max}|x_j|*\underset{i}{\max}\underset{j}{\sum}|a_{ij}|=||x||_\infty\underset{i}{\max}\underset{j}{\sum}|a_{ij}|$ чтд

$А$- точная матрица
$A^*$ - приближённая матрица
$\Delta A^*=||A-A^*||$
$\delta A=\dfrac{\Delta A^*}{||A||}\quad\delta A^*=\dfrac{\Delta A^*}{||A^*||}$