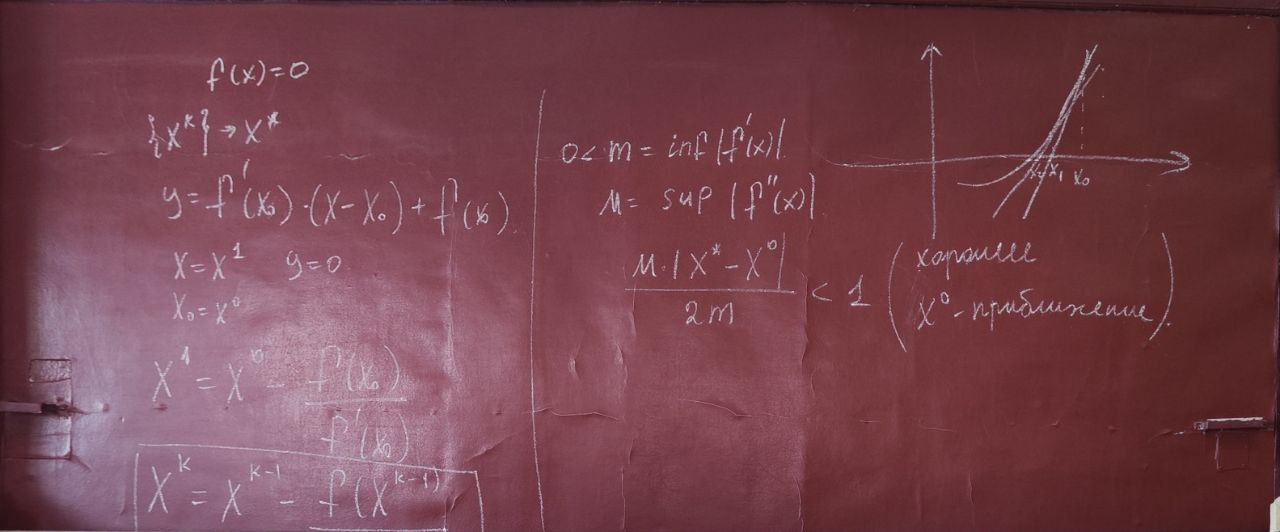Pasted image 20250328143724.png
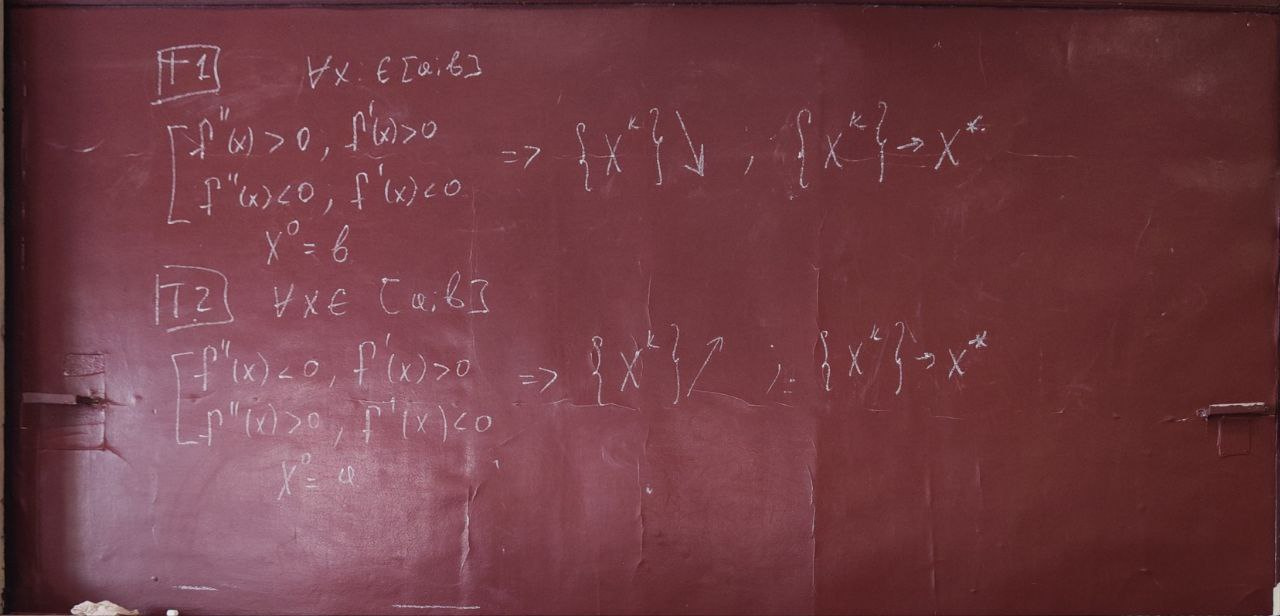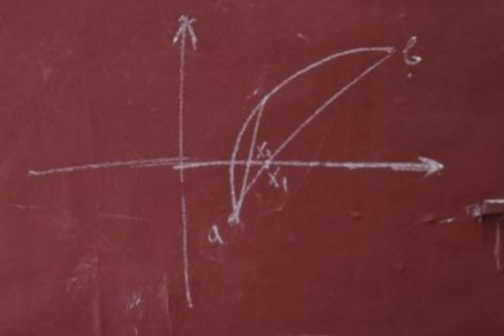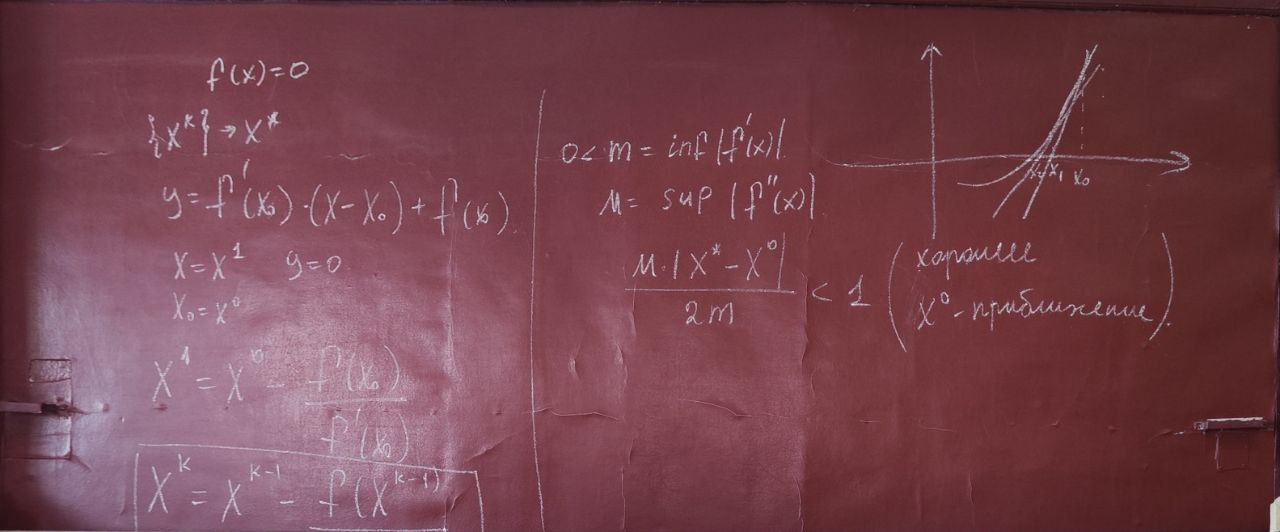
// My bad g, missed the beginning
..., тогда метод Ньютона сходится с квадратичной скоростью, и справедлива следующая априорная оценка: |Xk−X*|≤q2k−1*|X0−X*||X^k-X^*|\leqslant q^{2^k-1}*|X^0-X^*|
q=M*|X0−X*|2mq=\dfrac{M*|X^0-X^*|}{2m}
Метод Ньютона - квадратическая скорость сходимости
Теоремы 1-2
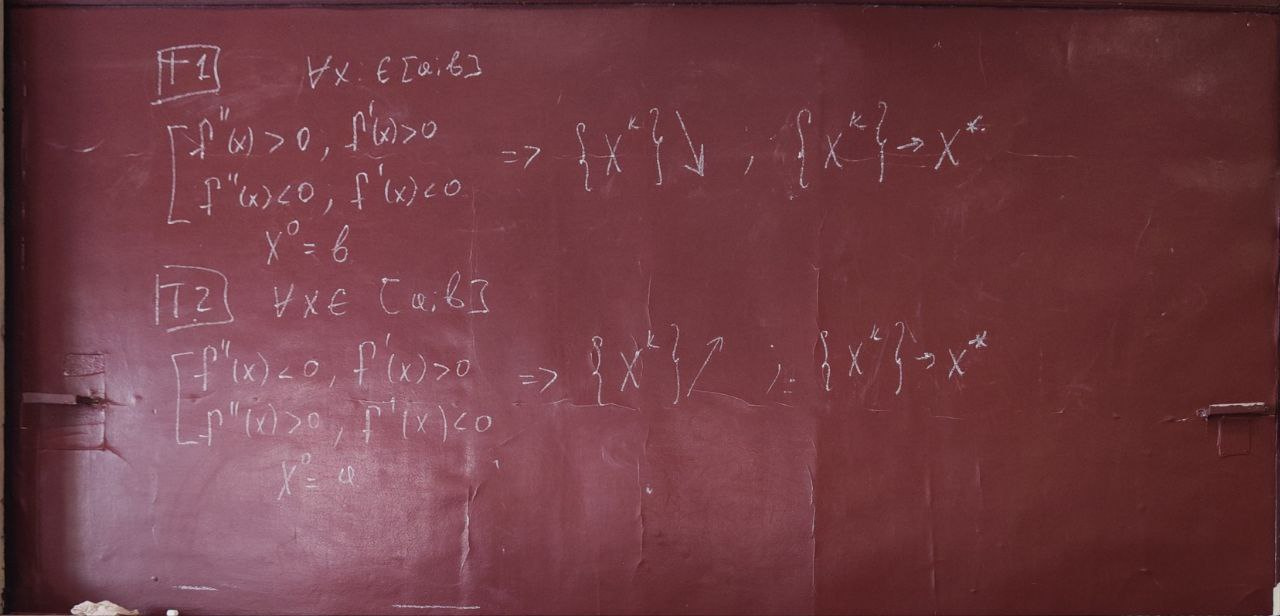
Pasted image 20250328144043.png
Доказательство теоремы 1
Пусть X*<Xk<bX^* < X^k < b
Тогда докажем, что если выполняется условие выше, то X*<Xk+1<XkX^*<X^{k+1}<X^k
Xk+1=Xk−f(Xk)f′(Xk)X^{k+1}=X^k-\dfrac{f(X^k)}{f'(X^k)}
Xk−Xk+1=f(Xk)f′(Xk)=f(Xk)−f(X*)f′(Xk)=f′(ξk)(Xk−X*)f′(Xk)X^k-X^{k+1}=\dfrac{f(X^k)}{f'(X^k)}=\dfrac{f(X^k)-f(X^*)}{f'(X^k)}=\dfrac{f'(\xi^k)(X^k-X^*)}{f'(X^k)}
0<f′(ξk)f′(Xk)<10<\dfrac{f'(\xi^k)}{f'(X^k)}<1
{xk−Xk+1>0Xk−Xk+1<Xk−X*→{Xk+1<XkXk+1>X*→X*<Xk+1<Xk\begin{cases} x^k-X^{k+1}>0 \\ X^k-X^{k+1}<X^k-X^*\end{cases}\to \begin{cases}X^{k+1}<X^k \\ X^{k+1}>X^*\end{cases}\to X^*<X^{k+1}<X^k чтд

Критерий окончания метода Ньютона

|Xk−Xk−1|<ϵ|X^k-X^{k-1}|<\epsilon

Трудности в использовании метода Ньютона

Модификации метода Ньютона

Упрощённый метод Ньютона

Суть метода - если производная непрерывна в окрестности корня X*X^*, то её значение вблизи этого корня можно считать почти постоянным
Производную считаем единожды в нулевом приближении
Xk+1=Xk−f(Xk)f′(Xk)X^{k+1}=X^k-\dfrac{f(X^k)}{f'(X^k)} - традиционный метод Ньютона
Xk+1=Xk−f(Xk)f′(X0)X^{k+1}=X^k-\dfrac{f(X^k)}{f'(X^0)} - упрощённый метод
Сходится тогда же, когда и метод Ньютона
Скорость сходимости - линейная, зато метод гораздо менее трудоёмкий
Pasted image 20250328151129.png

Метод секущих

f′(Xk)===f(Xk)−f(Xk−1)Xk−Xk−1f'(X^k)=^==\dfrac{f(X^k)-f(X^{k-1})}{X^k-X^{k-1}}
Xk+1=Xk−f(Xk)f(Xk)−f(Xk−1)(Xk−Xk−1)X^{k+1}=X^k-\dfrac{f(X^k)}{f(X^k)-f(X^{k-1})(X^k-X^{k-1})}
Двухшаговый метод, линейная скорость сходимости, трудоёмкость меньше метода Ньютона
Pasted image 20250328151137.png

Метод хорд

Усовершенствованный метод секущих - первая секущая проводится по отрезку локализации корня
Скорость линейная, зато что? Правильно, метод менее трудоёмкий
f(a)f(b)<0[a,b]f(a)f(b)<0\quad[a,b]
f(b)f″(x)>0→Xk+1=b−f(b)f(b)−f(Xk)(b−Xk)f(b)f''(x)>0\to X^{k+1}=b-\dfrac{f(b)}{f(b)-f(X^k)}(b-X^k)
Pasted image 20250328152321.png

f(a)f″(x)<0→Xk+1=a−f(a)f(Xk)−f(a)(Xk−a)f(a)f''(x)<0\to X^{k+1}=a-\dfrac{f(a)}{f(X^k)-f(a)}(X^k-a)
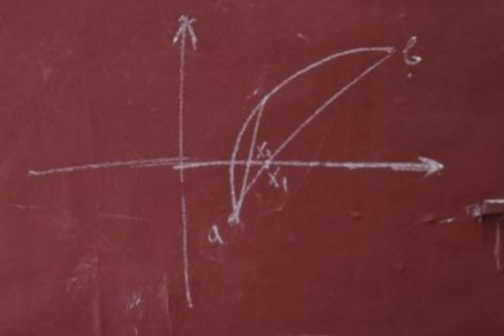
Pasted image 20250328152559.png

Методы аппроксимации функций

Постановка задачи - дана функция в виде таблицы, аналитического представления нет

x1x_1 x2x_2 …\dots xnx_n
y1y_1 y2y_2 …\dots yny_n
Задача - найти y=f(x)y=f(x) - перевести в аналитический вид
Вторая ситуация - есть ебейше сложная аналитическая функция, которую мы хотим заменить на более простое представление
Вычисление y=f(x)y=f(x) трудоёмко, поэтому нужно подобрать более простую функцию с наилучшим приближением к f(x)f(x)

Непрерывная аппроксимация

y=f(x)y=f(x) непрерывна на отрезке
y=ϕ(x)y=\phi(x) - функция аппроксимации
ρ|(f(x),ϕ(x)|=max|f(x)−ϕ(x)|→min\rho|(f(x),\phi(x)|=max|f(x)-\phi(x)|\to min - равномерное приближение